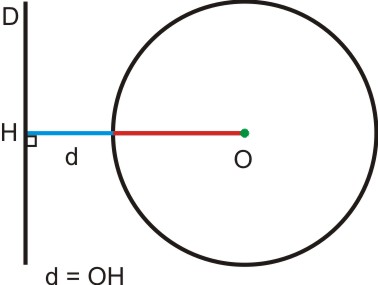
Seja O um ponto fora de uma linha D, tracemos a perpendicular OH à linha; meça a distância d do ponto O até esta linha. Descreve um círculo com centro O e raio R.
Dependendo das magnitudes relativas de R e da distância “d”, três casos podem ocorrer:
1º caso:
Se d > R, então a linha (D) está fora do círculo (C). Ou seja, a linha e o círculo não se encontram.
O ponto H é o ponto na linha D mais próximo de O. Agora está fora do círculo (C), do qual todos os pontos de D estão fora do círculo. Isso significa que a linha D está fora do círculo (C).
2º caso :
Se d = R, então a reta (D) é tangente ao círculo.
O ponto H é o ponto na linha D que está mais próximo de O. Mas está no círculo (C), o que significa que todos os outros pontos em D não estão no círculo.
Concluímos que a reta (D) é tangente ao círculo (C).
Propriedade : Se uma linha é perpendicular ao raio de um círculo em sua extremidade, então ela é tangente ao círculo.
Recíproca: Se uma linha é tangente a um círculo, ela é perpendicular ao raio que termina no ponto de contato.
3º Caso:
Se d < R, então a reta (D) é secante ao círculo.
o ponto H está dentro do círculo (C); portanto, a linha (D) divide o círculo.
A linha D e o círculo (C) têm dois pontos em comum e não podem ter outros. Dizemos que a reta D intercepta a circunferência (C).
Exercício
iniciantes 
tweeter compartilhar, distribuirExercício de matemática (matemática) “Posições relativas de uma linha reta e um círculo – lição” criada por patchy25 com O construtor de testes – crie seu próprio teste! [Plus de cours et d’exercices de patchy25]
Veja as estatísticas de aprovação para este teste de matemática (matemática)
Faça login em sua conta para salvar seu resultado.
Fim do exercício de matemática (matemática) “Posições relativas de uma linha e um círculo – lição”
Um exercício de matemática livre para aprender matemática (matemática).
Todos os exercícios | Mais aulas e exercícios de matemática (matemática) sobre o mesmo tema: Geometria
