Origami é a arte de dobrar papel, originária do Japão. A ideia desta atividade (realizada durante a semana de matemática, você pode aprender mais sobre o contexto neste outro artigo) é usar a dobra do papel para obter, depois de desdobrado, o desenho de uma geometria marcada figura. por dobras.
Regras do jogo : Temos uma folha de papel de qualquer tamanho na qual são colocados 2 pontos A e B.
Meta : construir dobrando um pentágono regular ABCDE .
Para construir dobrando, é necessário garantir uma certa precisão na confecção das dobras. Para isso, são permitidos apenas seis tipos de dobras, que definem a geometria do origami. Começamos descrevendo as dobras explicando a construção matemática que resulta delas. Em seguida, fornecemos um algoritmo para construir o pentágono regular a partir dessas dobras.
regras de construção de origami
Para cada dobra, o objeto geométrico correspondente é indicado. A seguir, a técnica de dobra é descrita através de uma série de etapas, a dobra obtida é representada por uma linha pontilhada no último desenho.
- dobrar d : uma única dobra passa por dois pontos A e B .
A dobra D é a linha (AB).
Técnica de dobragem:
- dobre m : um único vinco sobrepõe dois pontos dados.
A dobra M é a mediatriz de [AB].
Técnica de dobragem:
- dobra B : há uma dobra que se sobrepõe a duas linhas de interseção $∆_1$ e $∆_2$ .
A dobra B é uma das bissetrizes de $∆_1$ e $∆_2$.
Técnica de dobragem:
- P-dobra : uma única dobra passa pelo ponto A e é perpendicular à linha ∆.
Obtemos a reta perpendicular a ∆ que passa por A. A pode ser colocada na reta ∆.
Técnica de dobragem:
- c-fold : uma dobra, se existir, passa pelo ponto A e leva o ponto B à linha ∆.
O ponto $B_1$ em ∆ obtido tomando B em ∆ é um ponto de intersecção da reta ∆ com o círculo entre A e raio AB . Vemos o ponto $B_1$ por sobreposição, mas é necessário marcar este ponto com uma segunda dobra $P_1$ que passa por $B_1$ (independentemente de sua direção).
Técnica de dobragem:
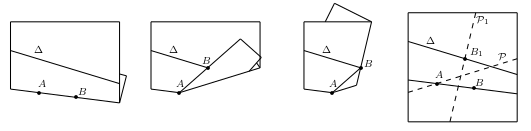
- dobrar ou : Uma dobra, se houver, traz o ponto $A_1$ para a linha $∆_1$ e traz o ponto $A_2$ para a linha $∆_2$.
A dobra O é a tangente comum às duas parábolas $P_1$ e $_P$2 com os respectivos focos $A_1$ e $A_2$ , e com a respectiva diretriz $∆_1$ e $∆_2$ . Esta linha não pode ser obtida pela construção de compasso e régua. É essa dobra que possibilita a construção de origami de objetos matemáticos que não podem ser construídos com régua e compasso como $\sqrt[3]{2}$.
Técnica de dobragem:
Este último O-ply específico para a construção dobrável não será utilizado para a construção do pentágono regular. De fato, o pentágono regular pode ser construído com régua e compasso. Em uma construção dobrável, usaremos apenas as cinco primeiras dobras.
Construção do pentágono regular dobrando um lado [AB]
Descrição da construção em 3 etapas:
- construção da proporção áurea $\Phi=\frac{1+\sqrt{5}}{2}$
- construção do triângulo isósceles ABD em D, graças à relação: $AD = \Phi\times AB$ (propriedade do pentágono regular)
- construção dos dois últimos pontos C e E do pentágono, por propriedades de simetria.
Estágio 1 : construção da proporção áurea $\Phi=\frac{1+\sqrt{5}}{2}$
-
Construção da praça da ABGF:
- uma dobra D para ter a linha (AB)
- uma dobra P de modo que a linha (AF) (perpendicular a (AB) passe por A)
- uma dobra P de modo que a linha (BG) (perpendicular a (AB) passe por B)
- a dobra B para construir a diagonal (AG) (bissetriz de (AB) e (AF)).
G é então o ponto de intersecção das duas últimas dobras.
-
Construção do ponto I da reta (AB) tal que $AD = \Phi\times AB$:
- uma dobra M para ter o ponto médio H e a mediatriz ∆ de [AB]
- uma dobra em C para trazer o ponto G para a direita (AB)
O ponto que obtive é então marcado com qualquer vinco.
A relação HI = HG e a aplicação do teorema de Pitágoras no triângulo BHG permitem mostrar que $AD = \Phi\times AB$
2º passo : construção do triângulo isósceles ABD em D
Esquecemos os pontos F e G desenhados anteriormente.
Dos pontos A, B, I e da reta ∆:
- uma dobra C passando por A e trazendo I sobre ∆ para obter o ponto D (marcamos o ponto D por qualquer dobra)
- uma dobra D para ter a linha (AD)
- uma dobra D para ter o direito (BD)
O comprimento AD é $\Phi\times AB$ .
etapa 3 : construção dos dois últimos pontos C e E do pentágono
Do triângulo isósceles ADB:
- uma dobra M para ter a mediatriz de (BD), denotada Γ
- uma dobra C passando por B para trazer A para Γ (marcamos o ponto C obtido por qualquer dobra)
- uma dobra P de modo que a perpendicular a Γ passe por C
- uma dobra M para ter a mediatriz de (AD)
O ponto E está na intersecção das duas últimas dobras.
E o polígono ABCDE é um pentágono regular.
